| Definitions | False, A  B, Rinit-v(x1), Reffect-f(x1), Rinit-discrete(A), Rinit-x(x1), Rinit?(x1), Reffect-discrete(A), eq_atom$n(x;y), Atom2Deq, Rsends-T(x1), Reffect-T(x1), Rsends-dt(x1), Rpre-a(x1), Rpre-ds(x1), Rpre?(x1), Rsends-ds(x1), Rbframe-L(x1), Rbframe-k(x1), Rbframe?(x1), Rsframe-L(x1), Rsends-knd(x1), Rsends-g(x1), Rsframe-tag(x1), Rsends-l(x1), Rsframe-lnk(x1), Rsframe?(x1), Rsends?(x1), Rrframe-L(x1), Reffect-ds(x1), Rrframe-x(x1), Rrframe?(x1), Raframe-L(x1), Raframe-k(x1), Raframe?(x1), Rframe-L(x1), Reffect-knd(x1), Reffect-x(x1), Rframe-x(x1), Rframe?(x1), Reffect?(x1), t.2, t.1, (i = B, Rinit-v(x1), Reffect-f(x1), Rinit-discrete(A), Rinit-x(x1), Rinit?(x1), Reffect-discrete(A), eq_atom$n(x;y), Atom2Deq, Rsends-T(x1), Reffect-T(x1), Rsends-dt(x1), Rpre-a(x1), Rpre-ds(x1), Rpre?(x1), Rsends-ds(x1), Rbframe-L(x1), Rbframe-k(x1), Rbframe?(x1), Rsframe-L(x1), Rsends-knd(x1), Rsends-g(x1), Rsframe-tag(x1), Rsends-l(x1), Rsframe-lnk(x1), Rsframe?(x1), Rsends?(x1), Rrframe-L(x1), Reffect-ds(x1), Rrframe-x(x1), Rrframe?(x1), Raframe-L(x1), Raframe-k(x1), Raframe?(x1), Rframe-L(x1), Reffect-knd(x1), Reffect-x(x1), Rframe-x(x1), Rframe?(x1), Reffect?(x1), t.2, t.1, (i =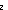 j), p j), p   q, R-interface-compat(A;B), R-discrete_compat(A;B), R-frame-compat(A;B), R-base-domain(R), p = q, Rda(R), Rds(R), R-loc(R), a = b, True, Rnone?(x1), Rplus-right(x1), Rplus-left(x1), P & Q, Rplus?(x1), ff, i <z j, q, R-interface-compat(A;B), R-discrete_compat(A;B), R-frame-compat(A;B), R-base-domain(R), p = q, Rda(R), Rds(R), R-loc(R), a = b, True, Rnone?(x1), Rplus-right(x1), Rplus-left(x1), P & Q, Rplus?(x1), ff, i <z j,   b, tl(l), i b, tl(l), i  z j, nth_tl(n;as), hd(l), z j, nth_tl(n;as), hd(l),  , {T}, SQType(T), , {T}, SQType(T),  A, Y, l[i], ||as||, tt, eqof(d), if b then t else f fi , Top, IdDeq, A, Y, l[i], ||as||, tt, eqof(d), if b then t else f fi , Top, IdDeq,   x. t(x), t x. t(x), t  T, T,  x x L. P(x), A || B, ( L. P(x), A || B, ( x,y x,y L. P(x;y)), Realizer, s.x, "$x", preinit1R{$x:ut2, $a:ut2}(i; X; p; x0; P), R-Feasible(R), P L. P(x;y)), Realizer, s.x, "$x", preinit1R{$x:ut2, $a:ut2}(i; X; p; x0; P), R-Feasible(R), P   Q, FinProbSpace, Q, FinProbSpace,  x:A. B(x), A c x:A. B(x), A c B, B,  , ,  x:A. B(x), P x:A. B(x), P    Q, Unit, (x Q, Unit, (x  l), P l), P  Q, i Q, i  j < k, Dec(P), {i..j j < k, Dec(P), {i..j }, x(s), State(ds), Normal(T), }, x(s), State(ds), Normal(T),  , S , S  T, T,  |